品質管理の基本|初心者に分かりやすいサイト > 正規分布と標準偏差|統計的品質管理
正規分布と標準偏差|統計的品質管理、3シグマ、分散、工程能力、CPK、PPKとは何か?など、統計的品質管理手法についての基礎的なこととを分かりやすく解説しています。
統計的品質管理とは?
品質管理をする上で、統計的品質管理手法の実施は避けて通れません。例えば、デイリー 数百個生産する部品を全数検査する事は不可能です。そのため統計的品質管理手法を用いて、少ない抜き取り数(=サンプル数)で、その母集団の平均やばらつきをより正確に推測する必要がありま す。例えば細長~い鉄板を50mmに切断していく機械があるとして、切断の公差が±1mmとして、抜き取って測定したデータの平均が50.2mmとしますね。バラつき(標準偏差)も小さいというデータであれば「これなら規格上限、下限まで余裕があるし、バラつき(標準偏差)も小さいので、規格外の製品が出る可能性は無さそうだな」という予想ができます。そうすれば全数検査しなくても、抜取で傾向をモニターしていれば大丈夫だな、と判断できます。
そのようなデータ管理をする為には、抜き取り方法(ランダムサンプリング等)、工程能力(CPK)、管理図による測定数値等のデータの変動を定常的に管理する等が必要です。このような考え方を総じて統計的品質管理手法と呼びます。
そして次章以降に説明していますが、その統計的品質管理を攻略するためのツールとして、「標準偏差」と「正規分布」が登場します。これは統計的品質管理においてセットだと思って下さい。学生時代のお勉強から、遠ざかっているサラリーマン(私もですが)には、ちょっと拒絶反応が出るかもしれませんが(^^;) 逆にこの2つさえ理解すれば、基本的にな統計的品質管理はほぼクリアです。
どうぞ気楽に臨んでください。
標準偏差=シグマ(σ)とは?|統計的品質管理
【σ:シグマとは】
シグマ=σ とは標準偏差のことで、「統計的品質管理」と言えばコレ、というくらい頻繁に使われる数値です。
データのバラつき具合を見る時に使う数値で、 個々のデータの、平均値からの差(=バラつき)の平均を言います。例えば、クラスの平均体重が「40kg」だとしても、35kg~45kgの間にかたまっている40kgなのか、下は25kgもいて、上は60kg近い子もいる40kgでは、分析する場合においてはエライ違いです。っという場合に用いるのが標準偏差=シグマ(σ)です。
算出方法についてはちょっと分かりにくいので、例を挙げてご説明しますね。
例)小学5年生の体重測定結果を以下のとおりまとめました。そして5人の平均は40kg、これは分かりますよね。次に「平均との差」これが個々のバラつきになりま す。そしてこの個々のバラつきの平均を出したのが、標準偏差=シグマ(σ)なのです。
| 氏名 | A | B | C | D | E | 平均 |
|---|---|---|---|---|---|---|
| 体重 | 43 | 29 | 35 | 51 | 42 | 40 |
| 平均との差 | 3 | -11 | -5 | 11 | 2 | 7.5 |
平均値(=40kg)からの差の平均である「7.5」が標準偏差となります。但し、算出方法がちょっと複雑で、単純に「(3+(ー11)+(-5)+11+2)÷5」ではないんです。算出式は以下の通りです。
※√は、ルートを表しています。
√((43-40)^2+(29-40)^2+(35-40)^2+(51-40)^2+(42-40)^2)÷5
です。つまり、個々のデータを平均値で引いて(43-40)、2乗する(9)。そしてそれを5個とも算出して(9+121+25+121+4)、足す。それを5で割る。(√280/5=56) そしてこの値は、最初に2乗したまま(√56)なので、最後にルートをルートを外すと、7.4833、、となり、上表の「7.5」というのが出てきます。ちなみにこの場合の「差の2乗の平均」(√を外す前の値)を【分散】と言い、統計学でよく使われます。
ちなみに【3シグマとは】
平均に対して大きい値もあれば小さい値もあるので通常は、±1σの事を「1σ」と言いいます。
上表では7.5ですが分かりにくいので、標準偏差(σ)を約「8kg」として、1σ=32~48kg
2σは1σの2倍なので=24kg~56kg そして「3σ」とは、この場合、16kg~64kg の間を指しま す。
正規分布とは?|統計的品質管理
【正規分布とは】
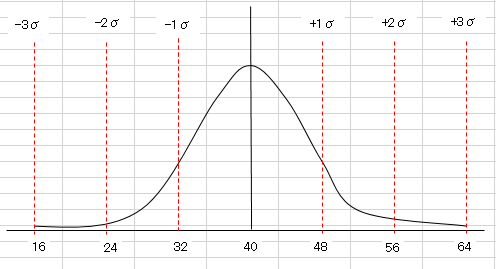
昔、賢い人が発見した分布(≒法則)で「標準偏差(σ)の1倍(1σ)に全体の約68%が存在し、2倍(2σ)に全体の約95%が、3倍(3σ)に99.7%が存在する」という法則のようなものです。よって、体重32kg~48kgの間には全体の68%が、24kg~56kgには全体の95%が、16kg~64kgには99.7%が存在しま す。(理論上)
自然界や社会の中で多く見られる現象で、 例えば図の体重の分布だと、平均が40kgくらいになり、極端に多い、少ない方向(64kgや16kgの方向)へ行くほど数は少なくなっていきます。あとは機械加工品のように、「一定の条件」で製品を作った場合も同様に平均値を頂点にして、上限/下限へいくほど数は少なくなっていきます。
そして n数が増えるほど、どんどん正規分布に近づいていきます。 (n が少ないと、1σで68%、、とはならないかも知れない。データ数が少ないと、真値とは遠くなりがちです)また、分布の形状としては、図のように平均値を頂点にして、左右に裾が均等に広がっていきます。平均が40kgくらいになり、極端に多い、少ない方向(64kgや16kgの方向)へいくほど数は少なくなりま す。
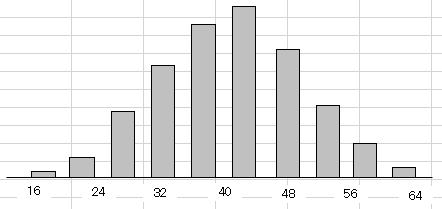
ヒストグラムを細かく細かくしていくと、下のような曲線になるイメージ。
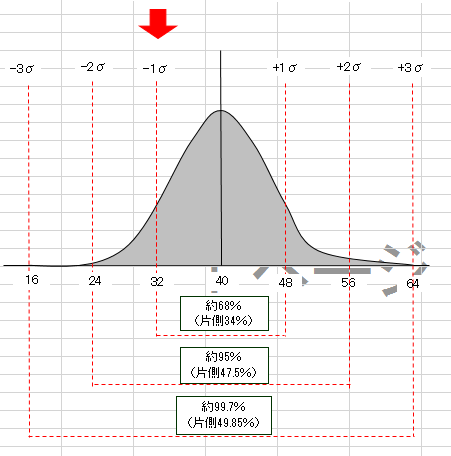
±1σ (標準偏差 2個分) に全体の 約68% が入る
±2σ (標準偏差 4個分) に全体の 約95% が入る
±3σ (標準偏差 6個分) に全体の 約99.7% が入る
±4σ (標準偏差 8個分) に全体の 約99.994% が入る事が、大昔の賢い人達によって証明されています。
また、正規分布にならない例として、学校のテスト等で難易度が高い場合、勉強してきた人とそうでない人で平均が分かれ、70点付近と40点付近などフタこぶラクダのように頂点が2つできる場合もありま す。
この場合「一定の条件」に当てはまらないというか、本来欲しいデータではない。グラフ上の高い山は、70点と40点付近だが、平均点は55点辺りになり、グラフでいうと、ちょうど谷にあたる部分になる。これがテストの点数の話ではなく、製品の測定値の場合、単に測定値の平均だけ見ると「何となく良さそう」と思ってしまうが、実際グラフに起こすと「何じゃこりゃ!」となります。
ちなみに工程で、測定値のグラフがフタこぶになったとなると、例えば、装置トラブルで途中から加工の位置がズレたとか、となりの規格の違う製品が混入した、等が考えられます。
話がやや脱線しましたが、統計学において「正規分布」していないと、ロジックが根底から覆りますのでご注意を、という話でした。