品質管理の基本|初心者に分かりやすいサイト > 実験計画法|方法、手順の例を紹介します
実験計画法|方法、手順の例を紹介します。実験計画法の考え方を解説します。実験計画法には様々な手法がありますが,ここでは,基本的な考え方を述べたいと思います。
実験計画法の考え方
【実験計画法の考え方】
次の3テーマについて解説していきたいと思います。
① 異常を検討する。
② 層別を検討する。
③ 平均とばらつきを同時に意識する。
実験計画法の考え方を解説します。実験計画法には様々な手法がありますが,ここでは,基本的な考え方を述べたいと思います。
1.層別の落とし穴
たびたび層別の意義や効用について述べてきました。その際,どちらかというと事後的な層別を考えてきました。事後的とは「データを採取した後」という意味です。ヒストグラムや散布図から層別の必要性が示唆される場合があります。グラフから示唆されなくても,
記録されている内容から,機械別,原料納入社別,作業者別,天気別,温度別,曜日別,昼夜別など,様々な層別因子に基づいて層別を試み,要因分析を行うことが望まれます。
しかし,層別してうまく違いが見出せたとしても,それで0Kということは必ずしもありません。たとえば.表.1に示す簡単なデータで考えてみましょう。表.1には部品Qの強度のデータと,そのデータに関連する層別因子として原料納入会社(2社,A1社とA2社),作業者(2人,B1とB2),製造機(2台,C1とC2)が記載されています。
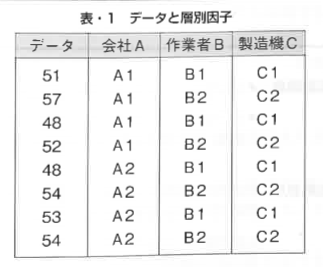
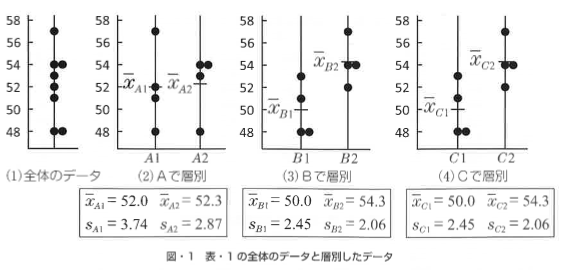
表-1のすベてのデータを図•1(1)に示しました。次に,原料納入会社別(Al, A2),作 業者別(Bl, B2),製造機別(Cl,C2)に層別した結果を図-1(2) (3)⑷に示しました。さ らに,層別したデータに基づいて平均と標準偏差を計算した結果も記載しています。
図-1(2)より,原料納入会社で層別しても違いはあまりないようです。一方,図-1 ⑶⑷より,作業者で層別した場合と製造機で層別した場合には,平均がかなり異なります。 作業者はB2の時,製造機はC2の時に強度が高くなっています。しかし,表-1のデータを 再度よく観察してみてください。表-1のデータでは,作業者がB1の時に製造機はC1,作業 者がB2の時に製造機がC2となっています。つまり,作業者の区別と製造機の区別が完全に 重なっています。したがって,層別後のグラフ,層別後の平均や標準偏差も,作業者と製造機 のそれぞれの場合で同じになっています。これでは,層別して違いを見いだせても,それが作 業者による違いなのか,製造機による違いなのか,その両方なのかはっきりしません。
実験計画法の必要性
6.2実験計画法の必要性
6.1節で述べた点は重要なので,同じ数値例を用いて詳しく 説明を続けます。表•1のデータを表• 2のように整理します。 これをBC二元表と呼びます。表.1や表• 2ではB1C2とB2C1 の組み合わせでデータがありません。したがって,作業者(B) と製造機(C}の効果の区別がつかないのです。これを「因子B と因子Cが交絡している」といいます。
ここで,表• 2のB1C2とB2C1の組合せでデータが観測さ れたと仮想してみます。いくつかの典型的なパターンを表•3 (1)(2) (3)に示します。「観測されたと仮想したデータ」を
太字のイタリック体で表示します。表• 3(1)(2) (3)において BとCの各組合せで平均を求めた結果を表.4 (1)(2) (3)に示 します。さらに,表-3と表-4を図-2⑴(2) (3)にグラフ化 します。